BS.AI®
 NOBEL PRIZE
NOBEL PRIZERewards are priced by our AI-driven Black-Scholes model (BS.AI)®, continuously learning from on-chain data.
 AI-DRIVEN
AI-DRIVENWe utilize the Nobel Prize-winning Black-Scholes model for pricing derivatives, a method trusted by major investment banks.
BS.AI® calculates trade rewards based on the expected profit. Orders are priced using BS.AI®, with payouts in pool tokens that support the token’s value.
Issued tokens are value - backed; the valuation of each order underpins their worth.
the
power
of
The Black–Scholes model was constructed as a so–called zero–sum game.
This means that if we consistently price user orders and pay for them according to the model, and then consistently settle the orders according to calculated price and settlement time, the long-term outcome will be zero – neither earning, nor losing (the value of paid rewards will be equal to the total income).
Our platform earns in the currency of the order, but pays in the$ $BRI token which is minted only when orders are placed. The value of placed orders creates in turn a fundamental value for $BRI tokens. In the long term BP’s revenue equals the value of all placed orders. It means that $BRI should be valued by the market according to the Black-Scholes model – as it will correspond to the cumulative value in the pool. It also allows Brightpool to incentivize stakers with the tokens traded on Brightpool such as WETH, USDT, USDC.
Price engine
The price engine is comprised of these two components (volatility algorithm & Black–Scholes model) and when combined, they are used to calculate the value of each order reward on our exchange.
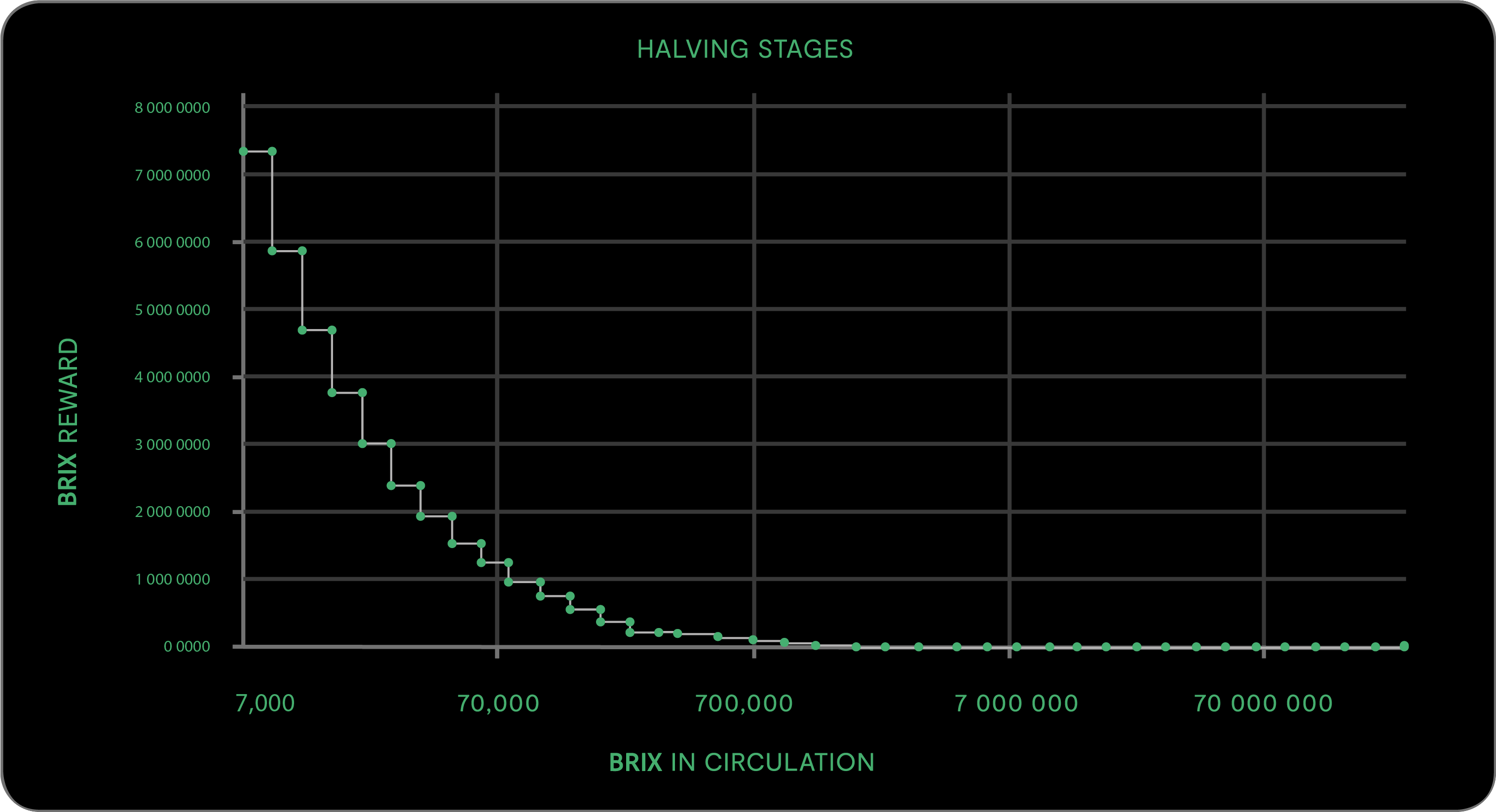
Rewards decrease through a steady reduction algorithm, similar to Bitcoin’s halvings – see the HALVING STAGES graph.
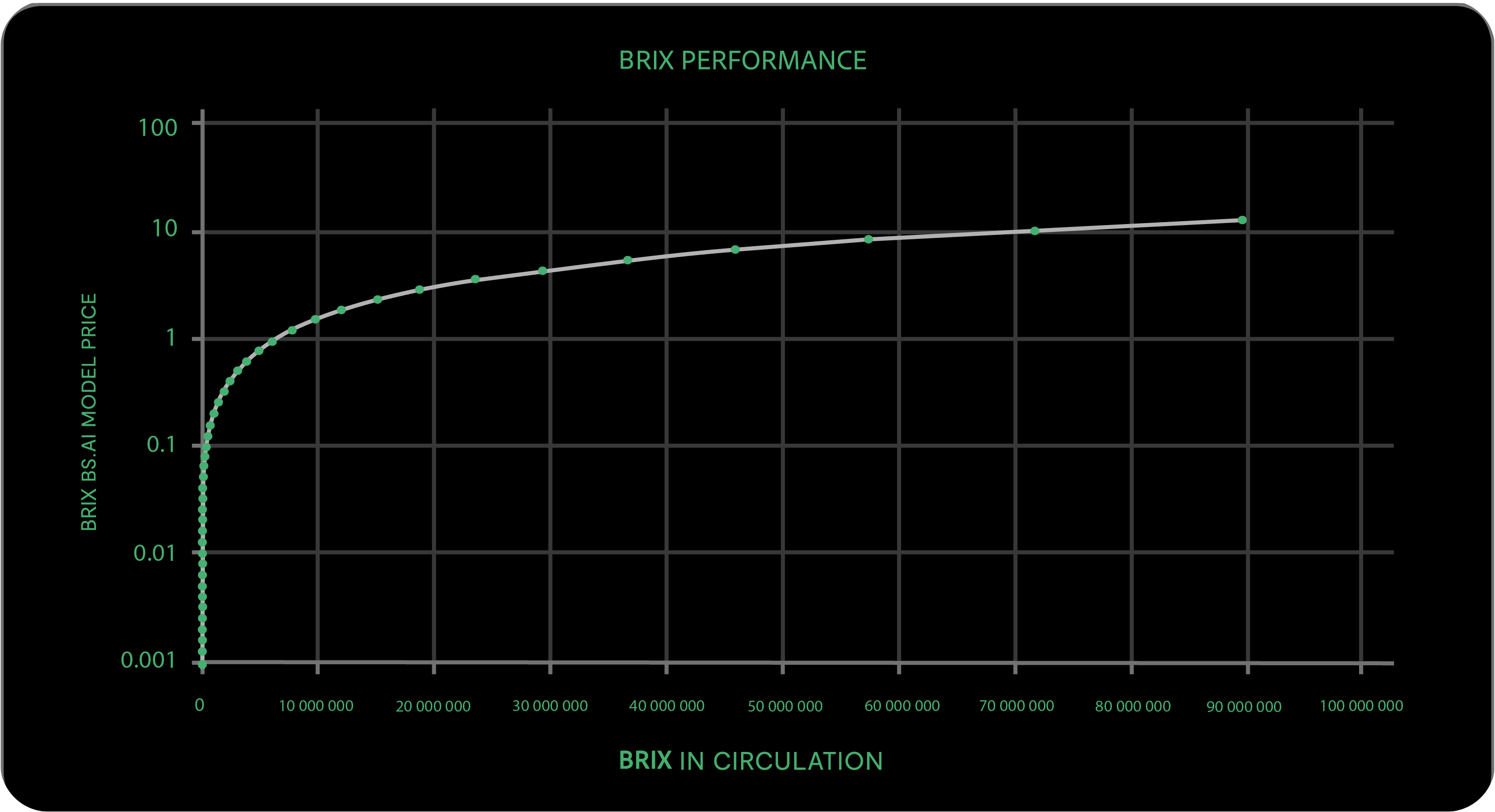
Early adopters earn more. The BRIX PERFORMANCE chart illustrates the value increase calculated by the BS.AI® model.
EARNON
VOLATILITY
BRIX token’s value is tied to Ethereum’s volatility.
Greater volatility leads to a higher token value.
BRIX would serve as the Volatility Index for ETH, similar to the VIX for the S&P 500 index.
Conclusion: Market extremes, be it a crash or boom, present unique additional opportunities. High volatility ignificantly boosts potential gains, positively impacting the project’s value and prospects.